Uninformed Search

Agents

An agent is a computer system that is capable of autonomous action in some environment. They work by observing the environment (through some sensor) and then perform actions (through some actuator) that change the environment until a goal has been reached. A rational agent will perform the action that will maximise its utility.

Reflex Agents

A reflex agent will only choose actions based on its current observation of the environment. They do not remember past environments or plan for the future. Often, reflex agents do not act rationally, it will depend on the initial environment.

Planning Agents

A planning agent is one that will look for possible future environments that may occur down the line and account for them. They may optionally choose the optimal solution. These are the types of agent we will use in search problems.

How to Search

Search problems have a list of States (known as the State Space), where an Agent starts at an Initial State and must make various Actions until it reaches a Goal State. A State is a description of the current environment. A transition model describes the effect of taking an action (e.g. Move from A to B, taking 10 minutes). Search problems may be described as a State Space Graph or as a Search Tree.

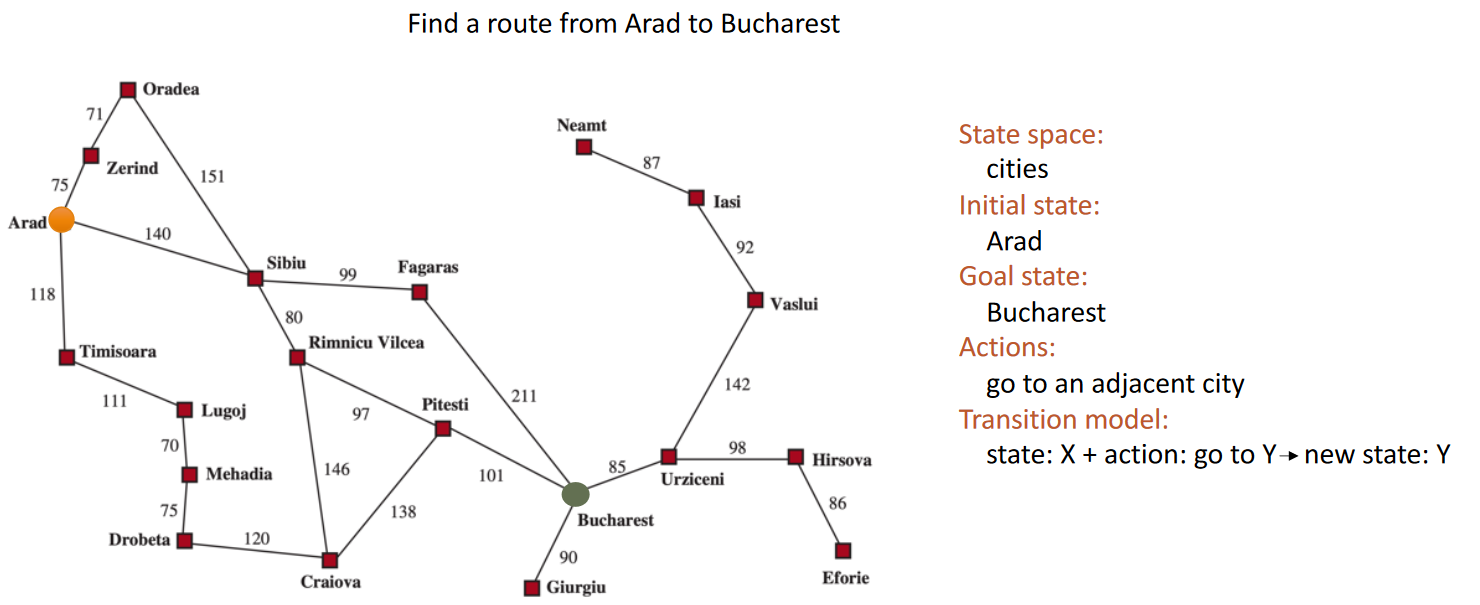
A sequence of actions forms a path. A path from the initial state to a goal state is a solution. A path with the lowest cost is an optimal solution.

How Search algorithms build Search Trees

First a node is "expanded" (this is when an agent observes the environment) - consider which actions can be taken and generate child nodes based on the resulting states. Generated nodes are called "reached". These states are added to the "frontier". A single node in the frontier is then explored (this is when an agent performs an action that affects environment). The process repeats until a goal state is reached or the frontier is empty (i.e. no solution).

Redundant paths may occur if there are multiple paths to reach a specific node or if there is a cycle (a path that starts and ends at the same node). Redundant paths may be avoided if the algorithm remembers which nodes have been explored and new nodes only being added to the frontier if they have never been explored. Algorithms which remember are called "Graph Search", while those that don't are called "Tree Search".

function TREE-SEARCH(problem) returns a solution, or failure
initialise the frontier using the initial state of problem
loop do
 if the frontier is empty then return failure
 choose a leaf node and remove it from the frontier
 if the node contains a goal state then return the corresponding solution
 expand the chosen node,adding the resulting nodes to the frontier

function GRAPH-SEARCH(problem) returns a solution, or failure
initialise the frontier using the initial state of problem
initialise the explored set to be empty
loop do
 if the frontier is empty then return failure
 choose a leaf node and remove it from the frontier
 if the node contains a goal state then return the corresponding solution
 add the node to the explored set
 expand the chosen node,adding the resulting nodes to the frontier
  only if not in the frontier or explored set

Algorithm Performance

There are 4 measures of algorithm performance, they are:

1. Completeness
   • Is the algorithm guaranteed to find a solution if one exists and to correctly report a failure if one doesn't exist?
2. Optimality
   • Will the algorithm find an optimal solution?
3. Time Complexity
   • How long will it take (measured in nodes)?
4. Space Complexity
   • How much memory is needed (measured in nodes)?

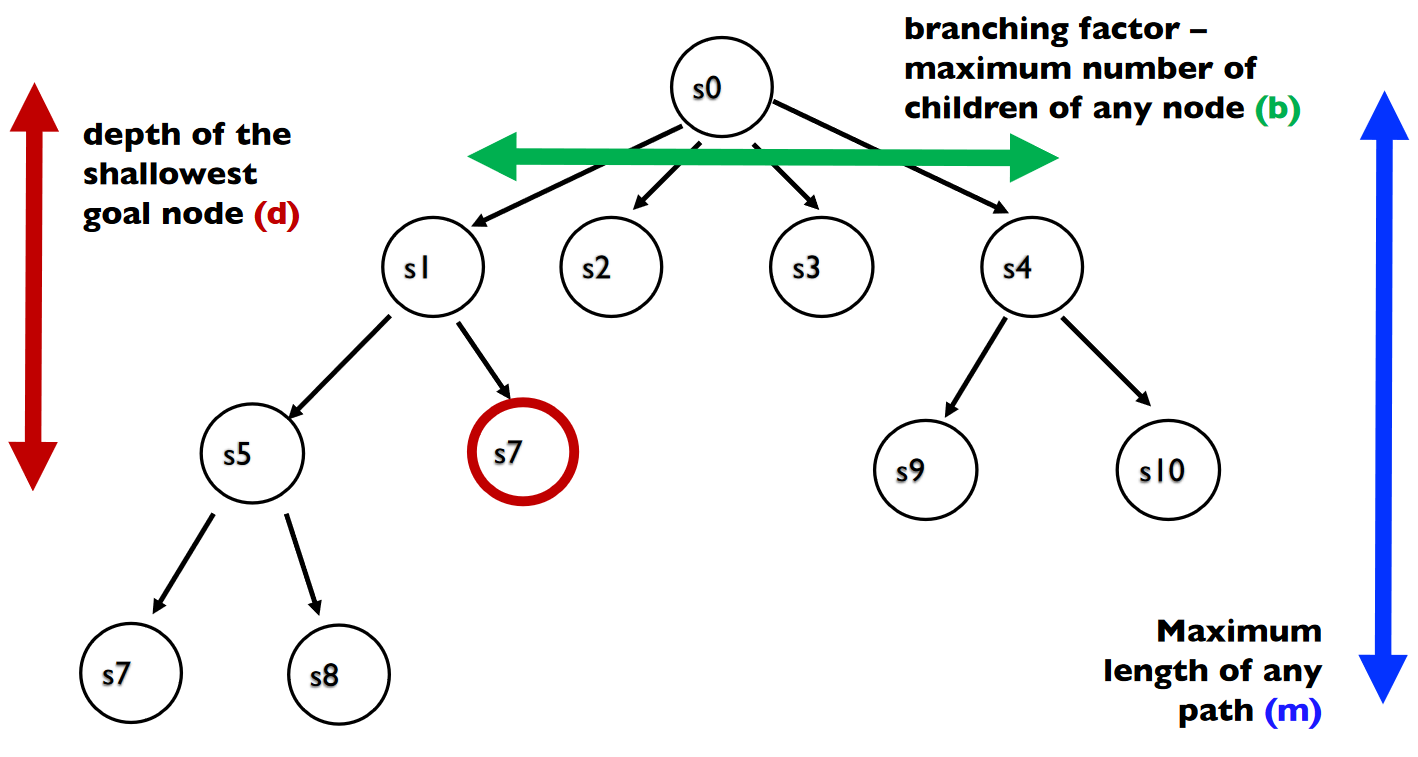
Complexity is often used in conjunction with the maximum branching factor (b), depth of the shallowest goal node (d), and maximum length of any path (m).

Search Algorithms

Here are a list of uninformed search algorithms and their properties. Search algorithms may have an early or late check. By which, an algorithm can check if a child node is a goal state before it is added to the frontier (early check) or the algorithm checks only after it has been explored (late check). Of these, Uniform Cost Search is the only one that must be late check, the others can be either.

Breadth First Search

In this algorithm, the shallowest node is the frontier is always explored first. If multiple of these nodes exist, then choose randomly.

This algorithm is complete and optimal if all actions have identical cost. It has a Time and Space Complexity of O(b^d) - which is a lot.

Depth First Search

In this algorithm, the deepest node is the frontier is always explored first. If multiple of these nodes exist, then choose randomly.

This algorithm is complete for finite tree-like state spaces (i.e. no cycles) but it is not optimal. It has a worst case Time Complexity of O(b^m) and Space Complexity of O(bm). The improved Space Complexity is the main selling point of depth first.

Iterative Deepening Search

Run depth first search with the maximum depth = 1 and iteratively increase the maximum depth until a solution is found. This is a sort of cross between breadth-first and depth-first.

This algorithm is complete for finite tree-like state spaces (i.e. no cycles) and optimal if all actions have identical cost. It has a Time Complexity of O(b^d) for problems with solutions. The Space Complexity is O(bd) for problems with solutions. Without solutions, replace the d with m (as all nodes must be expanded).

Bidirectional Search

Run iterative deepening search from start and goal, until the frontiers collide.

All properties are the same as iterative deepening search, except that the Time Complexity is O(2b^d/2). This is much less than O(b^d)

Uniform Cost Search (Dijkstra's algorithm)

In this algorithm, explore the cheapest node in the frontier. This is the only uninformed search algorithm in this list that considers the cost of actions.

Dijkstra's Algorithm is complete (if there is no cycle with zero cost) and optimal. It has a Time and Space Complexity of O(b^1+(C*/ε)). Where C* is the cost of the optimal solution and ε is the minimum action cost, where ε > 0.